一、导言
《运筹学》是管理类专业的重要必修课程。目前多数高校经济管理类专业的培养计划中设有此课程,但对于课程难度和深度要求、内容取舍以及学时安排没有不同看法和争论。
目前高校的《运筹学》教学大致有两种倾向:一种是强调课程学习对学生思维习惯和能力的训练培养,在内容选择和编排上以原理为主,更加注重理论研究;另一种则是强调课程的工具性质,内容以应用为主,引进计算机应用软件使用,将原理简化甚至不安排原理的教学。
以上两种做法能否满足我校人才培养要求,需要经过严格的论证。我校正在进行的本科人才培养规格第三层面设计,正是解决这一问题的重要举措。
二、本课程在专业中的地位
(一)本课程在学生知识、能力、素质培养中的作用
1.课程性质和基本目标
本课程是管理类专业的重要基础和常用工具,是一门重要的学科平台课程涵盖了线性规划及运输问题、动态规划、存储论、排队论等内容。本课程的学习将使学生掌握运筹学的基本原理和思想方法,树立优化决策的观念,为学习管理类专业的其他专业课程打下有益的基础。
2.课程对能力素质培养的作用
本课程重点培养学生基本的优化思维品质,教会学生用于计划编制、过程控制中常用的方法,培养学生运用管理数学方法解决实际问题的能力。
3.先修课程
高等数学、线性代数、概率论与数理统计
(二)本课程与其他主干课程的关系
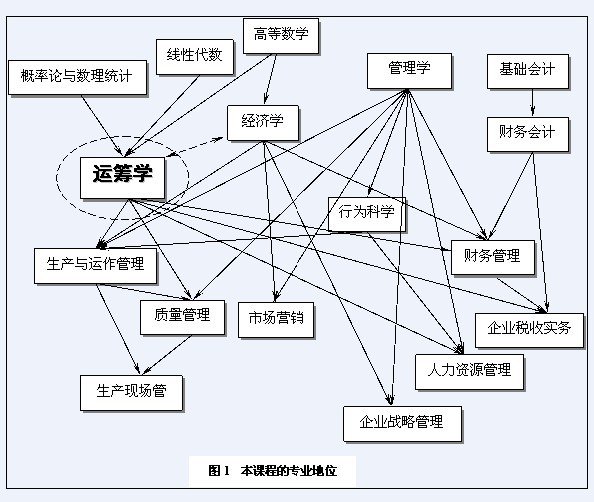
图1 本课程的专业地位
三、人才培养目标与规格解读
(一)工商管理专业(大类)培养目标
根据浙江树人大学教学型、应用型、民办性和地方性特点,以人为本,立足浙江,面向长江三角洲地区,培养适应21世纪经济建设和社会和谐发展需要的基础扎实、知识面宽、人格健全,具有较强适应能力、实践能力和创新精神,面向工商企业管理实际业务的复合型高级应用人才。
(二)对“高级应用型人才”的理解
“高级应用型人才”有别于研究型高校培养的“研究型人才”,也有别于高职院校培养的“应用型人才”。“高级应用型人才”首先应该具备应用能力,但同时必须是会研究和具备创新能力的,其研究是对应用的研究、对技术的创新和对各类技能的有效组合。这就有别于把理论研究和提升作为目标的“研究型人才”,同时也有别于把操作与熟练使用各类职业技能的“应用型人才”。
“面向管理实际业务”的内涵应是“对管理实际业务能在运用中进行优化”。
(三)“高级应用型人才”培养目标具体化
工商管理(大类)本科专业培养具备管理、经济、法律及企业管理方面的知识和能力,能在企、事业单位及政府部门从事管理工作的、德智体全面发展的、面向管理实际业务的高级人才。毕业生的定位是中层管理、现场管理及CEO助手。
(1)基本素质
具有坚定的政治方向和远大理想抱负,富有强烈事业心、责任心和创业精神,诚实谦逊,具有良好的社会公德和职业道德;具有健康体魄,自信自强,自主进取,具有良好心理品质。
(2)知识结构
了解社会科学、文化艺术方面的基本知识,具有一定的自然科学和技术知识,系统掌握管理学、经济学基础理论和学科发展动态,熟悉我国企业管理的有关方针、政策和法规以及国际企业管理的惯例与规则;熟悉管理技术和管理工具。
(3)能力结构
基本能力:学习能力、调查能力、分析研究能力、实践动手能力、沟通能力。
外显能力:掌握社交礼仪、具有计算机应用能力、具有英语一般阅读和运用能力、具有应用写作能力和文献查询能力。
能力专长:一般计划和制度编制能力、质量管理基本技术、会计核算和一般财务分析能力、会计电算化软件应用能力、一般营销策划能力。
四、本课程在培养规格实现中的作用
本课程教学在素质方面,立足于培养学生“优化”的思维习惯、系统化的全局观念、运用模型分析、问题的方法、运用模型分析问题的方法和严谨周到的流程设计思路。
在能力培养方面,侧重于上述“能力专长”的培养以及为“能力专长”的形成作准备。
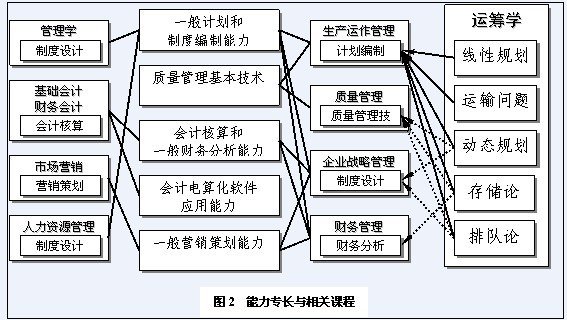
图2 能力专长与相关课程
五、课程内容与结构的内在设计
(一)运筹学学科的主要内容
运筹学按所解决问题性质的差别,将实际的问题归结为不同类型的数学模型。这些不同类型的数学模型构成了运筹学的各个分支。主要的分支有:
1.线性规划(Linear Programming)
经营管理中如何有效地利用现有人力、物力完成更多的任务,或在预定的任务目标下,如何耗用最少的人力、物力去实现目标。这类统筹规划的问题用数学语言表达,先根据问题要达到的目标选取适当的变量,问题的目标通过用变量的函数形式表示(称为目标函数),对问题的限制条件用有关变量的等式或不等式表达(称为约束条件)。当变量连续取值,且目标函数和约束条件均为线性时,称这类模型为线性规划的模型。有关对线性规划问题建模、求解和应用的研究构成了运筹学中的线性规划分支。线性规划建模相对简单,有通用算法和计算机软件,是运筹学中应用最为广泛的一个分支。用线性规划求解的典型问题有运输问题、生产计划问题、下料问题、混合配料问题等。有些规划问题的目标函数是非线性的,但往往可以采用分段线性化等方法,转化为线性规划问题。
2.非线性规划(Nonlinear Programming)
如线性规划模型中目标函数或约束条件不全是线性的,对这类模型的研究构成非线性规划分支。由于大多数工程物理量的表达式是非线性的,因此非线性规划在各类工程的优化设计中得到较多应用,它是优化设计的有力工具。
3.动态规划(Dynamic Programming)
动态规划是研究多阶段决策过程最优化的运筹学分支。有些经营管理活动由一系列相互关联的阶段组成,在每个阶段依次进行决策,而且上一阶段的输出状态就是下一阶段的输人状态,各阶段决策之间互相关联,因而构成一个多阶段的决策过程。动态规划研究多阶段决策过程的总体优化,即从系统总体出发,要求各阶段决策所构成的决策序列使目标函数值达到最优。
4.存贮论(Inventory Theory)
一种研究最优存贮策略的理论和方法。如为了保证企业生产的正常进行,需要有一定数量原材料和零部件的储备,以调节供需之间的不平衡。实际问题中,需求量可以是常数,也可以是服从某一分布的随机变量。每次订货需一定费用,提出订货后,货物可以一次到达,也可能分批到达。从提出订货到货物的到达可能是即时的,也可能需要一个周期(订货提前期)。某些情况下允许缺货,有些情况不允许缺货。存贮策略研究在不同需求。供货及到达方式等情况下,确定在什么时间点及一次提出多大批量的订货,使用于订购、贮存和可能发生短缺的费用的总和为最少。
5.排队论(Queuing Theory or Waiting Line)
生产和生活中存在大量有形和无形的拥挤和排队现象。排队系统由服务机构(服务员)及被服务的对象(顾客)组成。一般顾客的到达及服务员用于对每名顾客的服务时间是随机的,服务员可以是一个或多个,多个情况下又分平行或串联排列。排队按一定规则进行,如分为等待制、损失制,混合制等。排队论研究顾客不同输入、各类服务时间的分布、不同服务员数及不同排队规则情况下,排队系统的工作性能和状态,为设计新的排队系统及改进现有系统的性能提供数量依据。
6.对策论(Game Theory)
对策论也称博弈论,用于研究具有对抗局势的模型。在这类模型中,参与对抗的各方称为局中人,每个局中人均有一组策略可供选择,当各局中人分别采取不同策略时,对应一个收益或需要支付的函数。在社会、经济、管理等与人类活动有关的系统中,各局中人都按各自的利益和知识进行对策,每个人都力求扩大自己的利益,但又无法精确预测其他局中人的行为,无法取得必要的信息,他们之间还可能玩弄花招,制造假象。对策论为局中人在这种高度不确定和充满竞争的环境中,提供一套完整的、定量化和程序化的选择策略的理论和方法。对策论已应用于商品、消费者、生产者之间的供求平衡分析,利益集团间的协商和谈判,以及军事上各种作战模型的研究等。
7.决策论(Decision Theory)
决策是指为最优地达到目标,依据一定准则,对若干备选行动的方案进行的抉择。随着科学技术的发展,生产规模和人类社会活动的扩大,要求用科学的决策替代经验决策。即实行科学的决策程序,采用科学的决策技术和具有科学的思维方法。决策过程一般是指:形成决策问题,包括提出方案,确定目标及效果的度量;确定各方案对应的结局及出现的概率;确定决策者对不同结局的效用值;综合评价,决定方案的取舍。决策论是对整个决策过程中涉及方案目标选取、度量、概率值确定、效用值计算,一直到最优方案和策略选取的有关科学理论。
8.图论与网络分析(Graph Theory and Network Analysis)
生产管理中经常遇到工序间的合理衔接搭配问题,设计中经常遇到研究各种管道、线路的通过能力,以及仓库、附属设施的布局等问题。运筹学中把一些研究的对象用节点表示,对象之间的联系用连线(边)表示,用点、边的集合构成图。图论是研究由节点和边所组成图形的数学理论和方法。图是网络分析的基础,根据研究的具体网络对象(如铁路网、电力网、通信网等),赋予图中各边某个具体的参数,如时间。流量、费用、距离等,规定图中各节点代表具体网络中任何一种流动的起点、中转点或终点,然后利用图论方法来研究各类网络结构和流量的优化分析。网络分析还包括利用网络图形来描述一项工程中各项作业的进度和结构关系,以便对工程进度进行优化控制。
(二)《运筹学》教学内容取舍
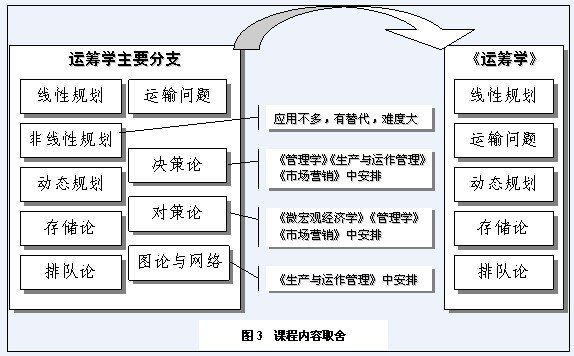
(三)课程建设策略
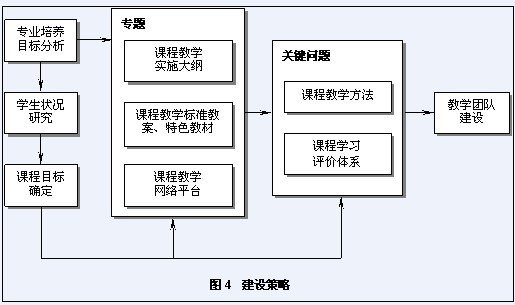
六、深度及难度处理典型实例
(一)线性规划的进一步研究:对偶原理
“对偶原理”是本课程中难度较大、对数学基础要求较高的内容,为此这一内容是否安排以及如何安排存在较多异义。我们作如下的分析:
运筹学实践中的两个问题:
第一,建模时,抽象与简化使模型与现实有了差距,这种误差应限制在什么范围?
第二,实际问题中的各种因素往往是变化的,这种变化对规划有什么影响?怎样才不影响原订的计划?
完整的决策模型应当对这些问题作出回答,这就是“灵敏度分析”,也称“敏感性分析”,研究各个决定模型结果的参数操纵模型结论的敏感程度。
稳定性差的和不可伸缩的模型及规划是没有现实意义和实用价值的,一般的系统模型都应进行灵敏度分析。而要学习灵敏度分析,就必须掌握“对偶原理”。
为了解决“易学”的问题,具体采用图形化处理的方法进行教学。
(二)马尔科夫过程的简化
在“排队论”模块中涉及随机过程的内容。为了满足“够用、易学”的要求,作了如下处理:
1.引入最简单流
第一,最简单流在现实中是大量出现的,因而具有广泛的应用价值;
第二,最简单流的数学处理方便,OR方法也最成熟;
第三,实际流与之有较大出入时,通过一定变换,仍可以从按最简单流处理的结果中得到所需精度的结论。
2.引入“生灭过程”
第一,状态平衡与状态转移的全概率描述;
第二,采用图形工具;
第三,利用“平衡”条件,将微分方程转化为线性方程;
第四,模型结论的程式化(标准化)。
七、《运筹学》课程实践环节
《运筹学》有较强的理论性,但同时也是与实践紧密结合的课程。为了加深学生对于运筹学方法的理解,达到“学以致用”的目的,我们安排了课外的实践环节。
主要有:“一个小应用”案例搜集、OR软件使用、人机对抗模拟决策实验。
八、教学实施
1.合作学习
合作学习(Cooperative learning)是一种旨在促进学生在异质小组中互助合作,达成共同的学习目标,并以小组的总体成绩为奖励依据的教学策略体系。
(1)分组原则
第一,原则上以寝室为单位分学习小组,每小组3~5人;
第二,小组长由小组成员轮流担当,轮换周期由各小组自行商定。
(2)成绩评定(供参考)
下列规则供参考,教师在实施过程中可以根据需要拟订规则,但必须在编制授课计划时先行确定,中途不得更改。
第一,总成绩:①课堂行为成绩(满分15分);②小组任务成绩(满分35分);③额外加分(累计不超过10分);④期末考试成绩(满分50分);⑤若四部分相加超过100分,总成绩以100分记;
第二,课堂行为成绩(“15分起平倒扣制”):①每生在15分的基础上,旷课一次扣1分,迟到一次扣0.5,上课睡觉一次扣0.5,穿拖鞋一次扣0.5;②一个小组每累积扣分达10分时,小组各成员扣1分;③每生剩余的分值便是其课堂行为成绩;
第三,小组任务成绩(“0分起平加分制”):①整个教学过程共布置6次小组任务,其中5次任务以“5分制”给予评定;1次任务为课程论文或市场调研,以“10分制”给予评定;②每次小组任务由小组成员合作完成,事先选定评价方式根据“小组任务评价原则”和“小组任务评价标准”评定小组得分,再由组长根据各组员在完成任务中的贡献大小,将组员数乘以小组得分的分值分配给各组员;③每生的各次得分总和便是其小组任务成绩;
第四,额外加分:①无扣分发生的小组,每位组员加2分;②小组取得值得推广的管理经验,每位组员加2分;③在课堂交流与课堂讨论中有突出表现的小组,每位组员加2分;④小组完成的论文有投稿价值,每位组员加3分;⑤公开发表论文的小组,视刊物的等级,每位组员加5~10分。
第五,期末考试成绩:①考试形式可以采用“一页纸开卷”;②卷面成绩采用“100分制”,并以50%的权重记入总成绩。
(3)小组任务及其评价
第一,小组任务类型:①论述问题;②资料收集;③案例研究;④主题研讨;⑤分章阅读;⑥案例撰写;⑦调研;⑧策划;⑨课程论文;
第二,小组任务成果:①书面材料;②案例;③课件;④调研报告;⑤策划案;⑥论文;
第三,小组任务评价原则:①事先确立评价标准,根据不同的任务类型,下达具体的评价标准;②人人参与,评价各组员是否都参与,是否各负其责;③内容相关,任务成果符合任务要求,并应用了课程知识;
第四,小组任务评价方式:①教师评价;②师生共同评价;③小组互评;④学生评价。
(4)小组成员惰化的控制
第一,组长轮流制;
第二,任务分解到人(各行其责);
第三,课堂问答抽查;
第四,任意选择汇报人。
(5)实施控制
合作学习教学模式采用“试点-总结-改进-推广”的分阶段实施路线,以课程为单位实施。凡采用合作学习教学模式的课程,主讲教师必须在学期初制订的授课计划中反映,并附加申请,经学院批准后方可执行。
合作学习课程由学院课堂教学质量评估小组负责日常检查。
2.团队教学
所谓团队教学也称“团队教学”或“协同教学”(Team teaching),就是由一两名或者更多教师共同参与同一课程的教学。这些教师本身都有相关专业的工作经验同时有各有所长,因而能够给予学生更实际更丰富的知识。
(1)适用范围
以下3类课程适合完全或部分采用团队教学:
第一,前沿性课程:一般指学科前沿介绍课程,涉及相关教师科研成果、研究方法的课程,如《管理学经济学前沿》等;
第二,综合性课程:一般指多学科交叉的课程,内容综合性强的课程,涉及相关教师研究领域的课程,如《广告学》、《管理与商务沟通》等;
第三,实务性课程:一般指应用性强的课程,直接涉及操作的课程,如《企业税收实务》、《投资与项目管理》等。
(2)课程组织
第一,设课程主讲教师1名,负责课程授课计划制订,讲课教师落实与安排,课堂管理,学生成绩评定,相关协调工作。
第二,课程内容根据大纲要求,原则上按专题进行模块化分解,不同专题模块可以由不同教师讲授。
第三,课程采用团队教学,模块划分及教师配备应当在其授课计划中体现,经教研主任及教学副院长批准,并在教学任务下达后方可实施。
第四,主讲教师对课程要有全程记录;其他教师授课时,主讲教师必须在场。
第五,学生的学习评价可以按模块逐项评定后进行综合,也可以一次性进行综合评定或者考核评定,但不论采用哪种方式,应当在设计时事先确定,并在授课计划中体现。
第六,采用团队教学的课程,原则上要求学生提交课程论文。
(3)实施控制
团队教学模式采用“试点-总结-改进-推广”的分阶段实施路线,以课程为单位实施。凡采用团队教学模式的课程,主讲教师必须在学期初制订的授课计划中反映,并附加申请,经学院批准后方可执行。
团队教学课程由学院课堂教学质量评估小组负责日常检查。
3.竞争性学习环境建设
(1)参与面广的课程竞赛
课程组每学年承办并组织“勤业杯”运筹学竞赛,管理学院工商管理、财务管理、市场营销三个专业、服务业学院物流专业以班级为单位组队参加竞赛。案例总数为10个,每个案例都有相应的分数,要求学生建立运筹学模型,并使用运筹学软件求解。以小组总分为评判标准,小组总分为组内各成员分数之和。最终决出一等奖、二等奖、三等奖和优胜奖。运筹学案例竞赛对锻炼和提高学生分析问题、合作共事和沟通交流的能力具有积极的作用。
(2)全国性的决策实践大赛
部分学生参加了由中国教育技术协会实践教学委员会、全国实践教学竞赛组委会主办,东华大学承办的全国管理决策实践大赛暨“东华杯”全国决策仿真大赛并取得佳绩,也促进了本课程的学习。
4.采用注重过程的考核方式
本学期课程的考核更加注重过程,总评成绩按以下方式核算:
总评成绩=平时成绩×30%+期中成绩×20%+期终成绩×50%
其中,平时成绩=每章作业成绩×60%+课程论文成绩×30%+竞赛加分 +出勤分
竞赛加分标准为:参与+2分,获优胜奖+4分,三等奖+6分,二等奖+8分,一等奖+10分
出勤分为缺席的扣分,为负值。
